第二節 資金的時間價值

由于房地產投資金額較大、投資期限較長，在進行投資分析和比較時，通常需要消除不同投資方案的費用、收入在時間上的差異，以保證每個投資方案在不同時間所發生的費用和收入具有可比性。為此，需要引進資金的時間價值這個概念。資金的時間價值以及資金等值計算的原理和方法，是進行房地產投資分析和比較所必需的基礎知識和基本技能。

一、資金的時間價值的含義

資金的時間價值也稱為貨幣的時間價值，是現在的資金比將來的等量資金具有更大的價值，通俗地說就是現在的錢比將來的錢值錢。這可以從銀行存款中得到簡單易懂的說明：你可以將現在立即得到的100元錢存入銀行，如果銀行存款年利率為5%，那么一年后你可以獲得5元的利息，該利息加上100元的本金共計105元。這樣，現在立即得到的100元錢在一年后就變成了105元。這意味著現在的100元等值于一年后的105元。反過來看，一年后的105元只相當于現在的100元;或者，一年后的100元只相當于現在的95. 24元(100÷1. 05=95. 24)。

進一步來看，表6-1中有A、B、C三個付款或投資方案，每個方案在未來3年的累計金額都是600萬元，但構成這600萬元的100萬元、200萬元和300萬元在未來3年發生的先后順序不同。如果此三個方案在其他方面沒有差異，則一般人憑直觀就可以判斷出它們的優劣次序。

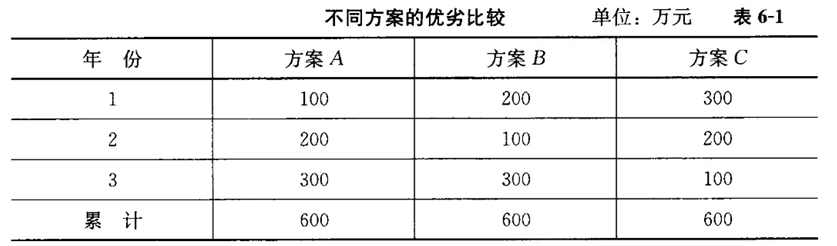
情形之一：如果是關于付款的方案，表6-1中的金額為付款額，則對于收款的一方來說，方案C優于方案B，方案B優于方案A;而對于付款的一方來說，方案的優劣順序則剛好相反。

情形之二：如果是關于投資的方案，表6-1中的金額為投資額，三個方案的投資收益和風險相同，則方案A優于方案B，方案B優于方案C。

之所以能夠輕而易舉地作出上述判斷，是因為在我們的腦子里已隱藏著資金的時間價值觀念。從經濟理論上講，資金存在時間價值的原因主要有下列幾個：

(1)資金增值。將資金投入生產或流通領域，經過一段時間后可以獲得一定的收益或利潤，從而資金會隨著時間的推移而產生增值。

(2)機會成本。機會成本(其他投資機會的相對吸引力)是指在互斥的選擇中，選擇其中一個而非另一個時所放棄的收益。一種放棄的收益就如同一種成本一樣。或者說，稀缺的資源用于某種用途意味著它不能用于其他用途。因此，當人們考慮使用某一資源時，應考慮它的第二種最好的用途。從這第二種最好的用途中可獲得的益處，是機會成本的度量。資金是一種稀缺的資源，根據機會成本的概念，資金被占用后就失去了獲得其他收益的機會。因此，占用資金時要考慮資金獲得其他收益的可能，顯而易見的一種可能是將資金存入銀行獲取利息。

(3)承擔風險。收到資金的不確定性通常隨著收款日期的推遠而增加，即未來得到錢不如現在就立即得到錢保險，俗話說“多得不如現得”就是其反映。

(4)通貨膨脹。現代市場經濟一般存在通貨膨脹。如果出現通貨膨脹，貨幣的購買力會下降，今天能用1元錢買到的商品或服務，以后很可能需要花不止1元錢才能夠買到。通貨膨脹會降低未來資金相對于現在資金的購買力，即錢不值錢了。

二、單利和復利

(一)利息和利率的概念

資金的時間價值是等量資金在兩個不同時點的價值之差，用絕對量來反映為利息，用相對量來反映為利息率(通常簡稱利率)。利息從貸款人的角度來說，是貸款人將資金借給他人使用所獲得的報酬;從借款人的角度來說，是借款人使用他人的資金所支付的成本。也可以將利息理解為使用資金的“租金”，如同租用房屋的房租一樣。利率是指單位時間內的利息與本金的比率，即：

計算利息的單位時間稱為計息周期，可以是年、半年、季、月、周、日等，但通常為年。習慣上根據計算利息的時間單位，將利率分為年利率、月利率、日利率等。年利率一般按本金的百分比來表示，月利率一般按本金的千分比來表示，日利率一般按本金的萬分比來表示。計算利息的方式有單利和復利兩種。

(二)單利的計算

單利計息是每期均接原始本金計算利息，即只有原始本金計算利息，本金所產生的利息不計算利息。在單利計息的情況下，每期的利息是相等的常數。

單利的總利息計算公式為：

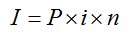
式中I——總利息;

P——原始本金;

i——利率;

n——計息周期數。

單利的本利和計算公式為：

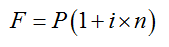
式中 F——計息期末的本利和。

【例6-1】將1 000元錢存入銀行2年，假如銀行2年期存款的單利年利率為6%，請計算到期時的總利息及本利和。

【解】到期時的總利息計算如下：

到期時的本利和計算如下：

(三)復利的計算

復利計息是以上一期的利息加上本金為基數計算當期利息的方法。在復利計息的情況下，不僅原始本金要計算利息，而且以前的利息都要計算利息，即所謂“利滾利”。

復利的本利和計算公式為：

復利的總利息計算公式為：

【例6-2】將1 000元錢存入銀行2年，假如銀行存款的復利年利率為6%，請計算到期時的總利息及本利和。

【解】

(四)單利與復利的換算

由上不難看出，在本金相等、計息周期數相同時，如果利率相同，則通常情況下(計息周期數大于1)單利計息的利息少，復利計息的利息多;如果要使單利計息與復利計息的利息相同，則兩者的利率應不同，其中單利的利率應高些，復利的利率應低些。假設i1為單利利率，i2為復利利率，并令n期期末時單利計息與復利計息的本利和相等，即通過

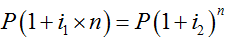
可得出單利計息與復利計息的利息相同的利率關系如下：

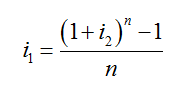
或者

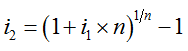
由于在通常情況下單利存款(定期)在存款期間不能隨意提取，流動性相對較差，所以為支付流動性補償，實際上的單利利率還應比上述計算出的單利利率高些。所謂流動性，是指在沒有太多損失的條件下，將非現金財產轉換為現金的速度。凡是能隨時、迅速且沒有損失或損失較小就能轉換為現金的，稱為流動性好;反之，稱為流動性差。

例如，某銀行存款的計息方式采用單利，假設其一年期存款的年利率為5%，為吸引3年期的儲戶，其3年期存款的單利年利率應大于：

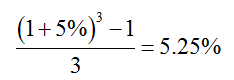
搞清楚了單利與復利的關系之后，便可知單利與復利并沒有實質區別，它們只是表達方式上的不同。利息計算在本質上屬于復利(否則可以在每一計息周期結束時將本利一起取出后再存入)，采取單利方式計息只是為了計算上的方便。

三、名義利率和實際利率

(一)名義利率和實際利率問題的產生

在上述利息計算中，是假設利率的時間單位與計息周期一致。當利率的時間單位與計息周期不一致時，如利率的時間單位為年，而計息周期為半年、季、月、周或天，就產生了名義利率和實際利率(也稱為有效利率)的問題。

(二)名義利率下的本利和計算

假設名義年利率為r，一年中計息m次，則每次計息的利率為r/m，至n年年末時，在名義利率下的本利和為：

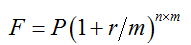
如果每半年計息1次，則m=2;每季度計息1次，則m=4;每月計息1次，則m=12。

(三)名義利率與實際利率的換算

要找出名義利率與實際利率的關系，可通過令一年末名義利率計息與實際利率計息的本利和相等來解決。

在名義利率計息下的一年末本利和為：

F=P(1+r/m)m

假設實際年利率為i，則在實際利率計息下的一年末本利和為：

F=P(1+i)

令一年末名義利率計息與實際利率計息的本利和相等，即：

P(1+i) =P(1+r/m)m

由上述等式可得出名義利率與實際利率的關系如下：

i= (1+r/m)m—1

【例6-3】年利率為6%，存款額為1 000元，存款期限為1年，如果按一年6%的利率計息1次，按半年3%(6%÷2)的利率計息2次，按季1.5%(6%÷4)的利率計息4次，按月0.5%(6%÷12)的利率計息12次，請計算這4種情況下的本利和及其實際利率。

【解】一年計息1次的本利和計算如下：

F =1 000×(1+6%)

=1060.00(元)

一年計息2次的本利和計算如下：

F =1 000×(1+3%)2

=1 060. 90(元)

一年計息4次的本利和計算如下：

F =1 000×(1+1.5%)4

=1 061. 36(元)

一年計息12次的本利和計算如下：

F =1 000×(1+0.5%)12

=1 061. 68(元)

這里的6%，對一年計息1次的情況來說，既是名義利率又是實際利率，對一年計息2次、4次和12次的情況來說，都是名義利率，而實際利率分別為：

一年計息2次：(1十3%)2 -1=6. 09%

一年計息4次：(1+1.5%)4 -1=6. 14%

一年計息12次：(1+0. 5%)12 -1=6. 17%

四、資金的時間價值的換算

(一)資金的時間價值換算的基本說明

1.資金時間價值換算中的符號及其含義

P表示現值，是指相對于將來值的任何以前時間的價值。

F表示將來值(也稱為未來值、終值)，是指相對于現值的任何以后時間的價值。

i表示利率(或稱為折現率)。

n表示計息周期數。

A表示等額年金，是指一系列每年相等的金額。年金最原始的含義是指一年支付一次，每次支付相等金額的一系列款項。但現在，年金被廣泛應用于其他更加一般的情形，如每季支付一次、每月支付一次或每周支付一次的一系列付款(或收款)都被視為年金。

2.資金時間價值換算中的假設條件

(1)資金時間價值換算中采用的是復利。

(2)利率的時間單位與計息周期一致，為年。

(3)本年的年末為下一年的年初。

(4)現值P是在當前年度開始時發生的。

(5)將來值F是在當前以后的第門年年末發生的。

(6)年金A是在每年年末發生的。

3.資金時間價值換算中的基本關系

現值十復利利息=將來值

(二)資金時間價值換算的常用公式

1.將現值轉換為將來值的公式

F=P(1+i)n

上式中的(1+i)n稱為“一次支付終值系數”，通常用(F/P，i，n)來表示。

【例6-4】某人向銀行貸款100萬元，貸款期限為3年，貸款年利率(復利)為8%，到期后一次性償還貸款本息。請計算到期后應償還的貸款本惠。

【解】到期后應償還的貸款本息計算如下：

1 000 000×(1+8%)3 =1 259 712(元)

2.將將來值轉換為現值的公式

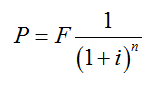
上式中的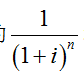 稱為“一次支付現值系數”，通常用(P/F，i，n)來表示。

【例6-5】年利率(復利)為8%，3年后500萬元的一筆收入在目前來看相當于多少萬元?

【解】該筆收入在目前來看相當于：

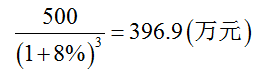
3.將等額年金轉換為將來值的公式

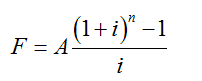
上式中的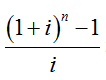 稱為“等額序列終值系數”，通常用(F/A，i，n)來表示。

【例6-6】某人每月向銀行存入100元錢，如果存款年利率(復利)為8%，按月計息，則20年后這筆錢的累計總額為多少元?

【解】20年后這筆錢的累計總額計算如下：

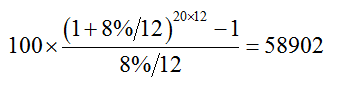
上述58 902元比20年內每個月100元的簡單加總額24 000元(100×12×20=24 000)要多一倍多。

4.將將來值轉換為等額年金的公式

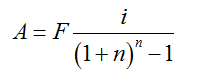
上式中的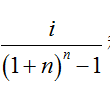 稱為“償債基金系數”，通常用(A/F，i，n)來表示。

【例6-7】某人打算每年向銀行存入一筆相同數額的錢，在10年后能攢到15萬元。假設存款年利率(復利)為8%，請計算該人每年應存款多少元?

【解】該人每年應存款計算如下：

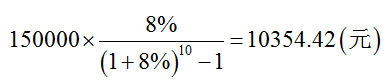
5.將等額年金轉換為現值的公式

上式中的 稱為“等額序列現值系數”，通常用(P/A，i，n)來表示。

【例6-8】某人欲購買一套住宅，最低首付款比例為20%。若該人用其積蓄按最低首付款比例交首付款，余款向銀行貸款，貸款期限為30年、貸款年利率為6%，按月等額償還本息;該人家庭月收入為5 000元，月收入的30%可用于償還貸款。請計算該人可承受的住宅總價為多少萬元?如果該人想購買一套建筑

面積為7 0m2的住宅，則該人可承受的住宅單價為每平方米建筑面積多少元?

【解】該人可承受的住宅總價計算如下：

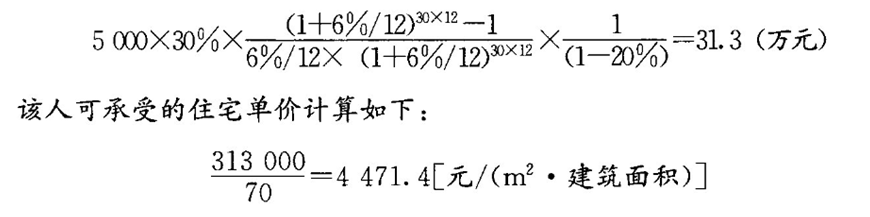
6.將現值轉換為等額年金的公式

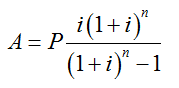
上式中的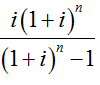 稱為“資金回收系數”，通常用(A/P，i，n)來表示。

【例6-9】某人購買一套總價為30萬元的商品住宅，首付款為總價款的30%，余款向銀行貸款，貸款期限為20年，貸款年利率為6%。如果按月等額償還貸款本息，請計算該人的月還款額。

【解】該人的月還款額計算如下：

編輯推薦：

房地產經紀人考試全方位輔導培訓資料

全國房地產經紀人考試歷年真題整理回顧

（責任編輯：）

共2頁,當前第1頁  第一頁  前一頁  下一頁